Computing Dense Hypersphere Packings in High Dimensional Space
If you've ever ordered fruits by the crate, you may be familiar with the sphere packing problem. Based on how they're arranged, the number of fruits that fit inside the crate varies; there are some arrangements that are, in some sense, denser than others. Now, instead of fruits, we're interested in figuring out how to densely pack high-dimensional hyperspheres.
The sphere packing problem is stated as follows: given some dimension
The sphere packing problem turns out to be very difficult for arbitrary
So what is a "dense" packing? To establish a baseline, let's first consider a trivial packing. If we place a sphere on every point of the
(this is simply the volume of an
We will consider lattices that satisfy this lower bound to be "dense" packings.
The proof of Minkowski-Hlawka is nonconstructive, meaning we don't know how to construct lattices satisfying the lower bound. However, Hlawka's proof guarantees that such a lattice exists within an exponentially-sized family of lattices, so at the very least we know that we are working with a computable problem.
Project Overview
My advisor and I were interested in assessing the computability of high-dimensional "dense" packings in practice. To do so, we focused on a family of lattices given by the following construction.
Fixing a dimension
where
Conceptually speaking, the family of
Unfortunately, a simple brute-force search over the
However, two questions may enable us to cut down the search space significantly:
- Can we learn from the geometry of the search space in low dimensions ro reduce the search space in high dimensions?
- If we fix a dimension
We have discovered evidence pointing to the affirmative in both cases.
Summary of Results
We begin by examining the 3-dimensional case. Since the 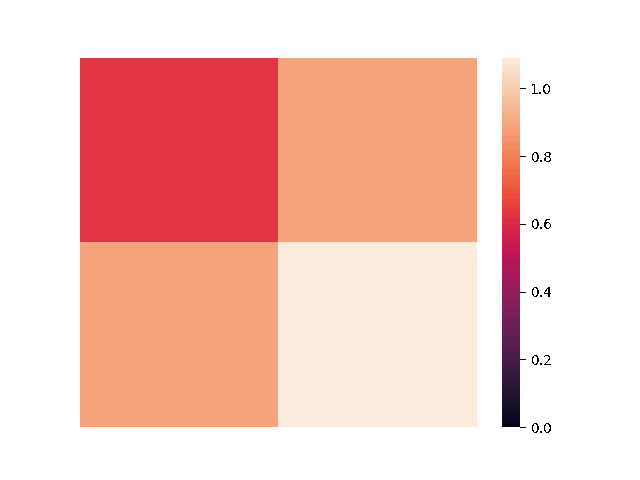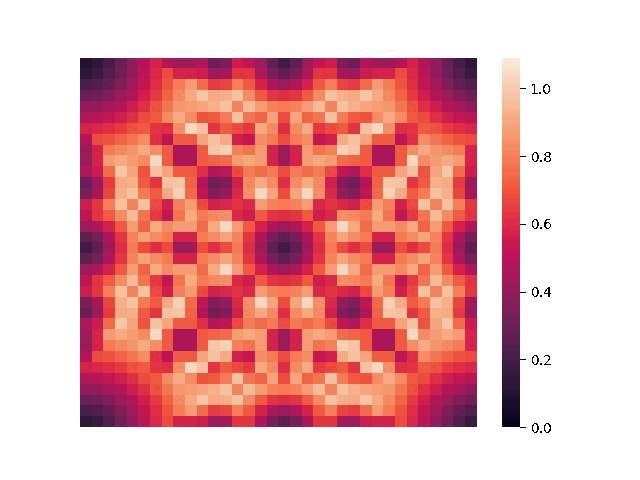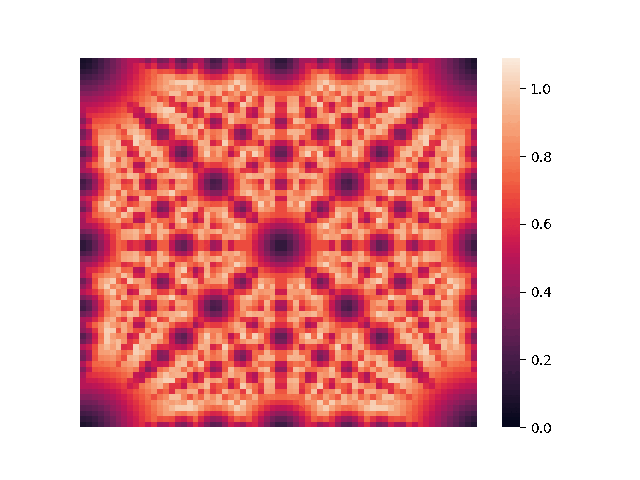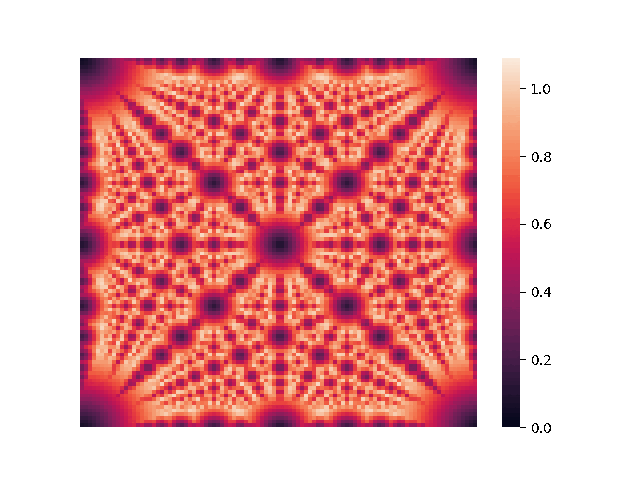
Here,
We also note that coordinates that are close to "simple fractions" produce sparse packings, although it's still unknown why this is the case.
These observations hold in four dimensions. Since the search space is 3-dimensional, we will fix a 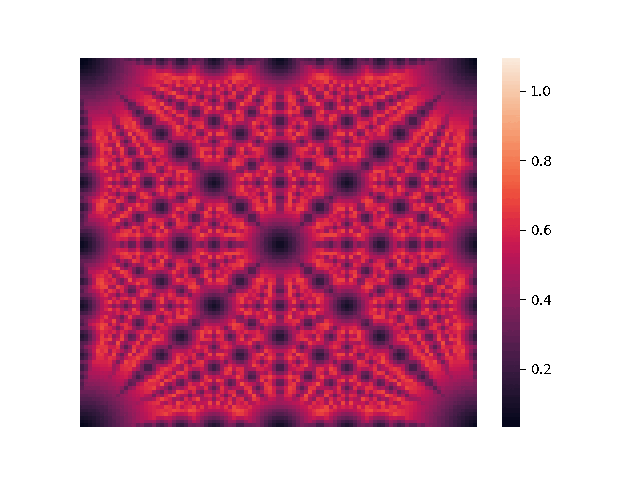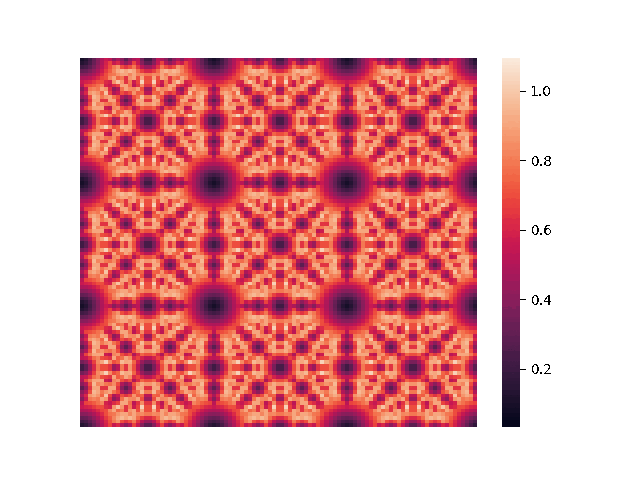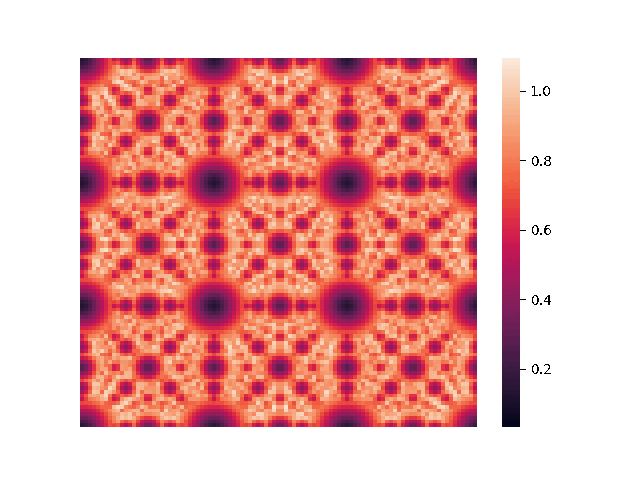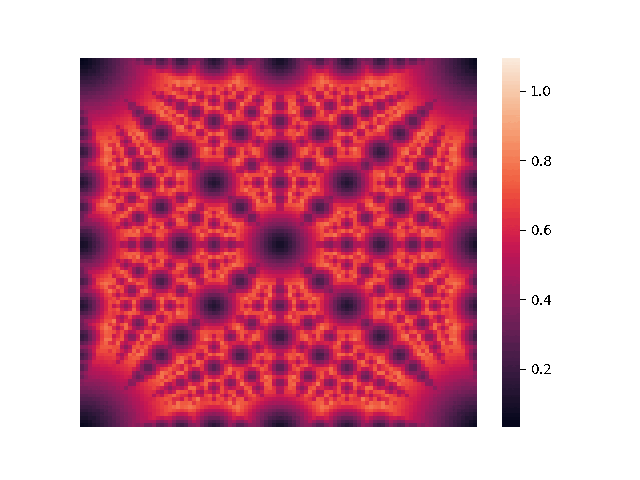
Relying only on symmetry, we are able to compute dense lattice packings up to
Beyond symmetries, we consider a number of search heuristics to further reduce the search space. In particular, we conjectured that