Message-Passing Networks

Graph Neural Networks (GNNs) have been cropping up everywhere in literature. They're a pretty neat concept, after all; graphs have wide coverage when it comes to encoding real-world data, so GNNs should, in theory, be very versatile models. But what exactly do they do? Why do they work? These are questions that we will explore in this post.

The Basics

GNNs are neural networks that operate on graphs; to be more specific, we're typically interested in simple undirected graphs.

Following convention, a simple undirected graph is a pair comprising a set of vertices and a set of edges . For a vertex , we let denote the neighborhood of , i.e. . Moreover, we typically want to associate each vertex with certain features, so let be the feature vector of .

The Message-Passing Framework

Gilmer et al. propose the Message Passing Neural Network (MPNN) framework as a generalization of various models for graph-structured data. For every vertex , MPNN computes a hidden state formalized by the following:

This one has a lot of components, so I will break it down piece-by-piece.

§ § §

Firstly, the MPNN framework is concerned with messages passed between adjacent vertices; computes the message from to .

notates a permutation-invariant aggregation operator (e.g. sum, max, mean, etc.) which, intuitively, aggregates all messages received by into a single signal.

is referred to as the update function, as it effectively updates the value of with the aggregated signal.

Both and are differentiable functions and typically compose a nonlinear activation with an affinity.

§ § §

That wasn't too bad, but what does this "message-passing" look like in practice? As a demonstration, I implement an—admittedly oversimplified*—MPNN as follows:

Instead of computing for all , we may leverage matrix operations:

where is the adjacency matrix of a graph with vertices, is the matrix of -dimensional feature vectors corresponding to vertices, and is the resulting matrix of embeddings. The corresponding Python code is incredibly succinct:

*A more practical implementation would involve a matrix of learnable parameters , and a nonlinear activation , e.g. , but they are not necessary for the sake of demonstrating forward-propagation behavior.

import networkx as nx
import numpy as np


def mpnn(a, h):
    return a @ h + h

g = nx.random_regular_graph(3, 10, seed=5)
a = nx.adjacency_matrix(g)
x = np.eye(10, 1)

h = mpnn(a, x)

Here, I generate a random three-regular graph with 10 vertices. One vertex is assigned a value of 1, while the others are zeroed. Here's what the graph looks like after a few successive passes through the MPNN:

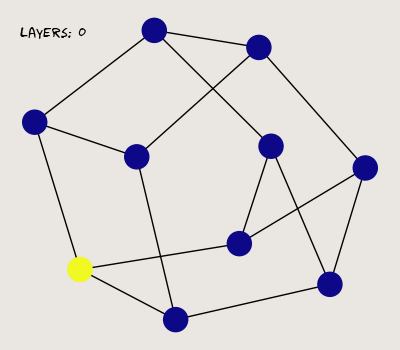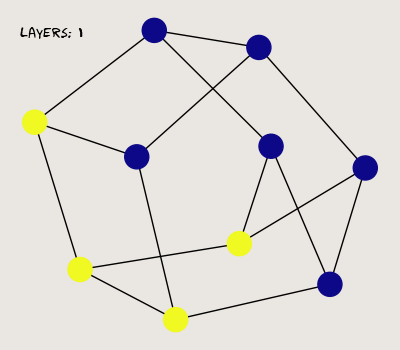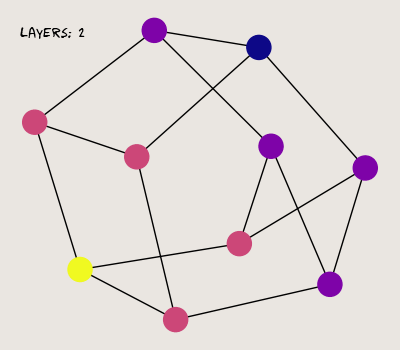
So far so good; our MPNN propagates a signal from each vertex to its neighbors. Now, let's see what happens when we stack more layers.

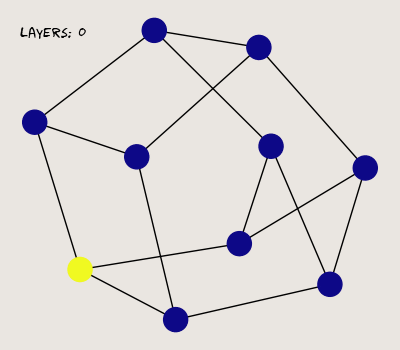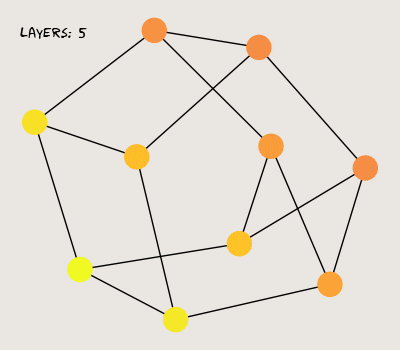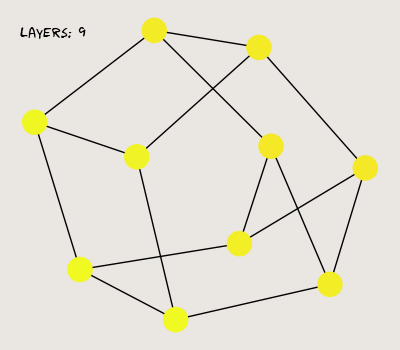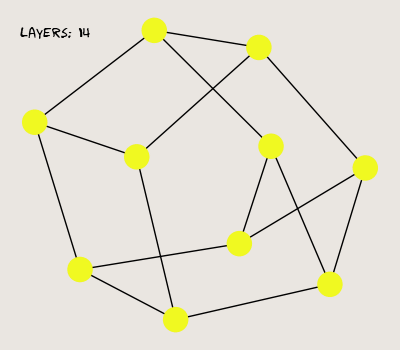
The graph's features seem to lose diversity when we add more layers; in fact, they converge regardless of the initial state (weights and nonlinear activations don't alleviate the issue). This behavior is known as the over-smoothing problem, where MPNNs lose expressiveness as more layers are stacked. Traditional neural networks, on the other hand, become more expressive with more layers. This paper does an excellent job of interpreting the mathematical principles behind over-smoothing, and it's a great bedtime read (joke).

For now, we can settle with shallow GNN architectures that use a small number of MPNN layers. I will investigate over-smoothing in more detail in a later post, but this is all I can handle in one sitting~

- Aaron